IV. Ligne Claire: lorsque la technique d'interaction créé l'outil

Ligne Claire est une technique d'interaction gestuelle destinée à circonvenir aux limites des techniques actuelles d'édition de courbes pour les graphistes professionnels. Ligne Claire est novateur sur deux aspects : les marques ne sont pas utilisées comme des raccourcis gestuels de commandes, mais pour spécifier des paramètres complexes qui ne pourraient être entrés de façon plus concise avec une autre technique. Enfin, cette technique constitue plus qu'un moyen d'édition : elle créé un style de dessin propre, comme une technique graphique (pastel, fusain, crayon...), facilite certains styles et types de dessin par rapport à d'autres. C'est en ce sens que Ligne Claire constitue autant une technique d'interaction qu'un outil de dessin particulier, avec ses contraintes et son langage graphique propres.

IV.1. Objectifs

Cependant la plupart (tous ?) des infographistes actuels n'utilisent pas ces logiciels au meilleur de leur capacités. Même les plus entraînés préfèrent esquisser et prototyper sur papier avant de digitaliser leurs brouillons plutôt que de concevoir leur oeuvres entièrement sur ordinateur, utilisant les possibilités de correction offertes par le logiciel. Certains logiciels, constatant cet état de fait, n'offrent aucune fonction permettant la correction partielle des courbes d'un dessin. TicTacToon [Fekete 1994], [Fekete, et al. 1995] destiné aux réalisateurs de dessins animés, est de ces logiciels, ses développeurs se justifiant par les observations suivantes :

* Les dessinateurs sont entraînés à dessiner sur un support ne permettant pas la correction, et font extrêmement peu d'erreurs : ils peuvent la plupart du temps dessiner du premier coup la forme qu'ils veulent représenter.

* Lorsqu'un dessin ne les satisfait pas, ils préfèrent effacer et redessiner tout ou partie du dessin, pour préserver un style de dessin propre et spontané.

* Fournir des possibilités de modification réclame l'introduction de modes et alourdit l'interface avec des fonctionnalités de toutes façons peu utilisables dans la pratique.

Les méthodes actuelles d'édition de courbes splines reposent sur le déplacement de points de contrôle et de tangence à la courbe. Elles ne répondent pas au modèle conceptuel que les graphistes peuvent avoir de leur tâche, car elles ont été conçues pour des utilisateurs ingénieurs et concepteurs industriels, dans un contexte spécifique [Bézier 1970]  :

* La représentation des points de contrôle permet une bonne spécification des contraintes que les objets conçus aux moyens d'outils de CAO doivent respecter : la position de chaque point peut être donnée avec précision, et les courbes splines utilisées ont souvent des caractéristiques géométriques utiles : C² continuité, approximation aisée de la surface ou du volume englobant...

* Les utilisateurs types ont un certain bagage mathématique leur permettant de comprendre certains aspects incohérents de la technique d'interaction. Par exemple, lorsqu'un point de contrôle est rapproché d'un point d'ancrage, des déformations très importantes de la courbe peuvent être obtenues par un déplacement de quelques pixels seulement du point de contrôle, produisant des sauts inattendus.

La technique d'interaction que nous avons conçue ne repose pas sur une représentation de données appropriée à un traitement informatique, comme les splines, mais sur l'extraction de schémas d'action des utilisateurs en contexte réel, en s'inspirant des techniques existantes. L'objectif est de fournir des techniques d'interaction appropriées puisque conçues "à façon" pour une catégorie d'utilisateurs donnée, tout en demeurant compatible avec les dispositifs d'entrée et les système informatiques actuels. Nous proposons une technique d'interaction pour l'édition de splines au moyen de la reconnaissance de marques tracées sur une tablette graphique, inspirée des techniques courantes d'édition de dessins papier. Après avoir situé le contexte de notre travail, nous exposons les observations que nous avons faites et en extrayons les concepts de notre techniques d'interaction. Nous décrivons ensuite les algorithmes qui permettent d'implanter efficacement cette méthode et les améliorations envisageables. Enfin, nous exposons un scénario d'utilisation nous permettant d'envisager une étude formelle d'évaluation. En conclusion, nous envisageons la création d'un modèle d'interaction complet utilisant notre technique pour permettre aux graphistes et aux artistes de créer et d'éditer des dessins au moyen d'outils informatiques plus appropriés.

IV.2. Méthodes actuelles d'édition de Spline

Plus récemment, Fowler et Bartels [Fowler et Bartels 1993] ont proposé une technique permettant la manipulation directe de splines, en déplaçant n'importe quel point de la courbe au lieu d'un ou plusieurs points de contrôle. Cette technique requiert cependant l'introduction de contraintes pour spécifier des invariances de tangence ou de position. Elle est partiellement implantée dans des logiciels de dessin actuels tel Canvasreg., et peut conduire à des méthodes d'interactions efficaces et plus naturelles.

Toutes ces représentations supposent que le périphérique d'entrée est une souris. Les outils de dessin professionnels utilisent cependant souvent une tablette graphique. Les courbes sont saisies par dessin direct, et la trajectoire échantillonnée est transformée en une représentation appropriée en utilisant un algorithme d'approximation de courbe comme celui de Schneider [Schneider 1990]. La tablette graphique est reconnue comme un dispositif d'entrée plus précis et plus efficace que la souris [Mackenzie, et al. 1991]. Les graphistes maîtrisent le dessin à main levée et ne se préoccupent pas des propriétés géométriques de leurs dessins ; aussi cette technique leur permet de créer de nouvelles courbes par le moyen le plus adapté et le plus direct qui soit. Cependant, aucune technique à notre connaissance de permet d'obtenir cette efficacité lorsqu'il s'agit de modifier une courbe existante.

En nous replaçant dans le contexte de l'interaction gestuelle, nous pouvons constater que dans tous les exemples précédemment étudiés, la forme des traces gestuelles est plus ou moins directement associée à une commande unique, les variations de taille, d'orientation et de position du geste servant parfois de paramètres simples ([Morrel-Samuels 1990], [Baudel et Beaudouin-Lafon 1993]). Dans notre cas, les marques sont utilisées pour entrer des données complexes de reparamétrisation plutôt que comme des raccourcis gestuels de commandes.

IV.3. Technique d'interaction gestuelle

IV.3.1. Un exemple du monde réel

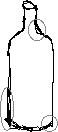
Figure IV.3.1 : Traits surchargeant le contour original (dans les ellipses grises)

Les dessinateurs professionnels s'entraînent longuement à ne pas utiliser instinctivement cette technique, pour éviter la lourdeur résultante des illustrations. Cependant elle est très naturellement utilisée par tous et peut fournir un bon modèle pour la modification de courbes : une fois entré dans un mode "modification", les marques sont interprétées comme des modificateurs de forme au lieu d'être de nouvelles courbes. Dans l'exemple suivant (la base de la lettre "i" en Times romain), des gestes successifs "tirent" la base de la lettre pour créer un sérif plus épais.

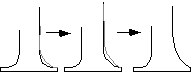
Figure IV.3.2 : Marques de correction successives (en gris) pour l'élargissement du sérif.

Nous utilisons des techniques de reconnaissance de geste, non pas pour reconnaître des commandes gestuelles, mais pour permettre la saisie de motifs de reparamétrisation complexes, qui ne pourraient être spécifiés avec un mode d'interaction plus simple. Cette technique repose sur et renforce un moyen naturel de modifier l'aspect visuel d'une courbe, et donc devrait être facile à assimiler pour un infographiste novice. De plus, cette technique est aussi appropriée pour des modifications locales que pour des reparamétrisations globales : un dessinateur peut entamer son oeuvre avec des gestes approximatifs de création et de reparamétrisation, pour obtenir rapidement une esquisse globale, puis raffiner progressivement ses gestes en convergeant petit à petit vers le résultat recherché. Cette approche descendante ne peut être obtenue avec les méthodes actuelles d'édition de Spline : l'utilisateur doit spécifier les points de contrôle un par un, ne peut changer leur emplacement sans artefacts sur la courbe et ne peut tester de changements importants en quelques actions simples et approximatives.

IV.3.2. Exemple d'application

Figure IV.3.3 : Effets d'un tracé dans chacun des 4 modes.

Dans certains cas, la cible de reparamétrisation (figure IV.3.4) peut ne pas être clairement déterminable. Dans ce cas, un micro-mode permet de supprimer les ambiguïtés : lorsque le système détecte plusieurs cibles possibles, il sélectionne les portions de courbes susceptibles d'être reparamétrées. L'utilisateur peut alors désigner la cible désirée pour exécuter la commande.

Figure IV.3.4 : deux courbes peuvent être reparamétrées. Le système présente les deux portions candidates et l'utilisateur peut cliquer sur celle qu'il désire reparamétrer.

Une véritable application requièrerait l'introduction d'interacteurs reflétant mieux l'état courant de l'interface : soit en utilisant des widgets conventionnels, menus et palettes, soit des techniques plus avancées, comme des outils transparents [Bier, et al. 1993],[Bier, et al. 1994]. Nous pourrions aussi considérer des techniques de reconnaissance de gestes pour différencier automatiquement les gestes de suppression des gestes de modification, ou utiliser des informations contextuelles pour unifier les modes "Modification" et "Jointure". Cependant, il est important de préserver la possibilité de dessiner n'importe quelle forme de reparamétrisation, sans déclencher de jointure, ou supprimer un trait qu'on désire reparamétrer. Des modes clairement identifiés sont peut être dans ce cas le meilleur moyen d'éviter des conflits entre l'intention de l'utilisateur et l'interprétation du système. L'utilisation de modes peut se rapprocher de l'utilisation de différents instruments physiques que peut utiliser un graphiste : divers types de crayons, gommes, pinceaux... les fabricants de tablettes graphiques actuels, comme Wacom, fournissent à l'heure actuelle divers types de stylets permettant de reproduire une interaction avec des objets physiques proche de l'environnement de travail des graphistes, et à même de refléter au mieux les différents modes d'un outil de dessin informatique.

IV.4. Implantation

IV.4.1. Notation

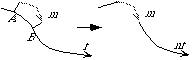
Figure IV.4.1 : Reparamétrisation d'une courbe f.

Cette opération se fait en deux étapes:

* Trouver la cible f dans F et les paramètres A et B dans [0..Lf] qui se rapprochent le plus de m. Il faut pour cela définir une distance entre des portions de courbes qui corresponde à notre perception visuelle.

* Étant donnés f, A , B et m, transformer f en fonction du mode courant pour obtenir nf. Plusieurs méthodes peuvent être employées, sans qu'aucune ne semble plus appropriée.

IV.4.2. Détermination de la cible

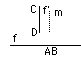
Figure IV.4.2 : un cas pathologique: m est perpendiculaire à f.

Soit d une distance entre deux points (nous utilisons l'approximation d(f(t),m(u)) = (fx(t)-mx(u))²+(fy(t)-my(u))²). Pour tout couple (u,v) de [0..Lf]², on défini la distance D entre fuv et m comme la somme infinitésimale des distances entre chaque point de fuv et son point correspondant sur m :

(a)

La portion de f "visuellement la plus proche" de m est fAB telle que [[universal]] (u, v) [[propersubset]] [0..Lf]², D(fAB,m) <= D(fuv, m). La courbe cible pour la reparamétrisation est f dans F pour laquelle il existe (A,B) qui minimise cette distance pour toutes les courbes de F. On notera que le couple (A,B) n'est pas forcément ordonné : B peut être un indice sur f supérieur ou inférieur à A. Lors de la minimisation de l'équation (a), il convient donc de tester toutes les valeurs possibles des couples (A,B) : si A>B, alors m et f sont tracées dans le "même sens", sinon, elles sont tracées en sens contraire. Enfin, dans la pratique, on conserve toutes les courbes en-deçà d'un certain seuil comme des candidats possibles pour permettre à l'utilisateur de reparamétrer des courbes proches l'une de l'autre en sélectionnant la cible désirée.

Si f et m sont des suites continues de segments (polylignes) sans boucles, il est possible de trouver les paramètres A et B qui minimisent cette distance en un temps directement proportionnel au nombre de segments. Pour cela, on suppose dans un premier temps que A=B. On obtient ainsi un polynôme du second degré pour chaque segment (formule b), qui peut être minimisé en temps constant. Le point résultant se trouve au milieu des portions de courbes qui minimisent la formule (a) localement. On dispose ainsi de bons points de départ pour des techniques de minimisation locales, telles que la méthode du simplex [Press, et al. 1991].

(b)

Cette technique permet la sélection de cibles en temps réel, pour des dessins de quelques milliers de segments, en utilisant seulement une fraction de la puissance de calcul, même sur des machines de performance modeste comme un Macintosh utilisant un processeur 68020. Il est possible d'optimiser le calcul en utilisant des patchs de Bézier quadratiques au lieu de convertir les splines en suites de segments avant la sélection de la cible. Par contre, l'utilisation de patchs cubiques ne devraient pas améliorer le temps de calcul, puisqu'il faudrait alors minimiser des polynômes de degré 6 : il n'existe pas de méthode algébrique générale de résolution de ces équations, aussi une méthode d'approximation ne devrait rien apporter.

IV.4.3. Reparamétrisation

Au premier abord, on peut considérer que la transformation doit conserver le nombre et la position des points d'inflexion de f sur [0..A] [[union]] [B..Lf]. Cependant, cette condition ne peut être toujours vérifiée. De plus, notre technique d'interaction rend cette condition relativement inutile : elle encourage soit des marques de reparamétrisation importantes mais imprécises, soit des marques courtes et rapides, mais précises, qui commencent et finissent sur la courbe à reparamétrer, "tirant" progressivement la courbe vers la forme désirée (figure IV.4.3). Dans ce cas, les transitions entre f et nf sont minimes et les points d'inflexions sont conservés là où ils doivent l'être.

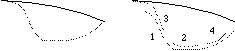
Figure IV.4.3 : Lorsque l'on désire une modification importante, il est plus aisé de faire de petites corrections rapides, qu'un seul grand trait de reparamétrisation requérant plus de précision.

La méthode que nous employons actuellement est simple à implanter, bien qu'elle puisse introduire des points d'inflexions superflus. En supposant que A<B et en nous donnant une constante k (pour l'instant 3), qui représente la "douceur" de la transition, et un polynôme de transition P(x) = -2x³+3x² (il est possible d'utiliser d'autres fonctions pour introduire un biais ou produire des effets spéciaux. Dans tous les cas, il faut que P(0)=0 et P(1)=1 pour préserver la continuité de nf). La reparamétrisation de f commence au point S= A - k.d(f(A), m(0)). Si S est négatif, m est dit "marque de prolongation" : nf démarre en m(0) et il n' y a pas de transition entre f et m sur [0..A]. Sinon (figure IV.4.4, partie droite), on définit le segment mS, prolongation de m de longueur (A-S), de pente m'(0) et tel que mS(A-S)=m(0).

Figure IV.4.4 : Exemple de reparamétrisation. m et f sont artificiellement écarté afin de rendre le dessin plus clair. Habituellement, m(0) et f(A) sont plus proches, ce qui supprime le point d'inflexion entre S et A'.

La transition de f à nf est obtenue en interpolant mS avec les points de f sur [S..A] :

pour chaque t dans [S..A] fait

coeff = P((t-S)/(A-S));

nf(t) = (1-coeff)*f(t) + coeff*mS(t-S)

fin de boucle

Les valeurs de P sur [0..1] permettent de préserver la continuité C² de nf , partout où f et m sont C². La transition réciproque de m(Lm) à f est obtenue de la même façon en posant E = B + k.d(f(B), m(Lm)). Si E<Lf, on interpole fBE avec mE, prolongation de m ; sinon (figure IV.4.4, partie gauche), m est une "marque de prolongation" et nf se termine en m(Lm). Cet algorithme c'est avéré satisfaisant en pratique, bien que la transition ne soit pas toujours suffisamment "douce" lorsque fAB et m sont trop éloignés. De plus, il est possible de paramétrer la "douceur" de transition en utilisant les informations de pression sur le stylet fournies par la tablette graphique.

IV.4.4 Implantation complète

IV.4.4.1 Algorithme de suppression partielle

IV.4.4.2 Jointure de courbes

Il n'est pas trop difficile d'étendre les possibilités de jointure de courbes à un nombre arbitraire de courbes. Il convient pour cela de concevoir un algorithme de choix des courbes cibles explorant parmi les candidates ceux qui ont une extrémité visuellement proche de la courbe modificatrice m. Le développement du modèle d'interaction impose cependant d'autres priorités.

IV.4.4.3 Traitement des courbes fermées

La suppression d'une portion de courbe fermée a pour seul effet de l'ouvrir à nouveau. Les courbes fermées ne sont pas intégrées dans l'ensemble F des cibles potentielles dans le mode de jointure de courbes.

IV.5. Première évaluation

Figure IV.5.1 : Tâche d'approximation de courbe. Le "&" sert de modèle.

Avec notre technique, cette tâche devient très simple à réaliser : il suffit de redessiner sur les contours du modèle. Les copies d'écran suivantes sont réduites à 20%. L'écho des marques de reparamétrisation est montré en gris pâle. L'utilisateur commence par enlever les sérifs avec deux marques qui reparamétrisent les deux extrémités de la lettre (figure IV.5.2), puis des marques qui ajustent les contours plus précisément.

Figure IV.5.2 : Les trois premières marques: suppression des sérifs

Le contour extérieur est approché par quelques marques longues (5), puis des marques plus précises, qui suivent les contours du modèle (figure IV.5.3).

Figure IV.5.3 : Ajustement des contours extérieurs

Les contours extérieurs sont ajustés en 4 ou 5 marques (figure IV.5.4).

Figure IV.5.4 : Reparamétrisation des contours intérieurs

Quelques marques supplémentaires ajustent avec précision les portions de courbes restantes, permettant d'obtenir le résultat final (figure IV.5.5).

Figure IV.5.5 : Résultat final

Une meilleure précision peut être obtenue en "zoomant" sur les portions imparfaitement alignées et en corrigeant les courbes avec de petites marques précises. Cependant, notre maquette ne permet pas le zoom. En supposant que la main ne peut réaliser efficacement des ajustements de moins de 2 pixels, la résolution courante est d'environ 40 dpi. Le temps nécessaire à l'obtention d'une telle précision est légèrement inférieur au temps nécessaire pour redessiner toute la courbe avec un logiciel tel que FontStudio, pour un utilisateur expert. Cependant, une bonne approximation est obtenue en quelques marques, même par un dessinateur inexpérimenté. Nous pensons que les graphistes, nos utilisateurs cibles, sont moins contraints par ces limites, parce qu'ils n'ont pas besoin d'obtenir une résolution supérieure à ce qu'il peuvent voir et contrôler avec leurs outils conventionnels.

De plus, la possibilité de faire des transformations globales en une seule action permet à l'utilisateur de suivre une approche descendante, à partir d'esquisse rapides, puis de raffinements successifs, plutôt que d'avoir à décider au fur et à mesure de la position de chaque point de contrôle et les changer un par un pour atteindre la forme recherchée. La transparence de cette technique d'interaction permet à l'utilisateur de se concentrer sur le but à atteindre, sur le langage des formes entre elles, plutôt que d'être encombré de considérations de détail, comme la recherche par essais et erreurs des paramètres de chaque point de contrôle.

Le commentaire principal que nous avons obtenu d'utilisateurs dans un contexte de test informel est une demande d'écho supplémentaire. Lorsque'une modification est réalisée, la position de la courbe précédente est immédiatement effacée. Or la recherche d'une forme idéale se fait souvent par essais et erreurs sur un grand nombre de courbes proches les unes des autres. Nous pouvons par conséquent envisager d'estomper progressivement les courbes modifiées, en offrant en quelque sorte un historique visuel des modifications apportées. L'apport de cet historique est un exemple d'écho sémantique s'étendant au delà d'une commande simple.

IV.6. Conclusion et perspectives

* Évaluation ergonomique : Notre première évaluation nous a permis de constater les limites des tâches d'approximation de formes pour l'évaluation de notre technique, puisqu'on ne peut comparer une modification à l'aide de notre technique avec une re-création au moyen des techniques traditionnelles. Nous entreprenons des procédures d'évaluation plus formelles, aussi bien avec des utilisateurs avertis qu'avec des graphistes ne connaissant pas la manipulation des courbes de Bézier. Ceci doit nous permettre d'améliorer les algorithmes de reparamétrisation pour prendre mieux en compte l'effet recherché par une marque de reparamétrisation.

* Utilisation des informations de pression : Les applications de dessin telles que Painterreg. utilisent les informations de pression sur le stylet pour permettre des variations de texture ou de densité du trait. A l'heure actuelle, nous ne connaissons pas de technique d'interaction permettant de changer ces paramètres en même temps que la forme d'un trait. Nos algorithmes n'utilisent pas les informations de pression à l'heure actuelle, mais notre technique pourrait être utilisée pour éditer texture et épaisseur.

* Extension du modèle d'interaction : Notre maquette se concentre à l'heure actuelle sur la technique d'interaction plus que sur l'articulation des modes entre eux au sein d'un modèle d'interaction global. Nous comptons étudier des mécanismes tels que le changement automatique de mode, l'écho du mode courant et l'intégration des changements d'attributs graphiques (couleurs, motifs...) au moyen d'outils d'interaction transparents (étudiés qu chapitre suivant). Nous disposerions alors d'un nouveau paradigme pour le dessin à main libre qui devrait mieux satisfaire les besoins actuels.

Ligne Claire propose un nouveau paradigme d'interaction pour l'édition de splines, reposant sur une technique de reconnaissance de marques qui permet une reparamétrisation directe au lieu de la modification individuelle de points de contrôle. Cette technique est implantée au moyen d'algorithmes efficaces qui permettent l'identification et la reparamétrisation de la cible en temps réel. Une évaluation informelle nous a montré les avantages suivants:

* Interaction Naturelle: reposant sur l'observation des méthodes usuelles des graphistes, cette technique fournie la base d'un modèle conceptuel plus naturel pour l'édition de splines.

* Interaction Rapide: Une bonne approximation de la forme recherchée peut être obtenue rapidement et affinée à un degré arbitraire de précision. Cela permet une approche de conception descendante, par esquisses et retouches, plutôt que la construction progressive (point par point) d'un dessin final difficile à éditer.

* Interaction Conforme: La technique de reconnaissance de marques permet l'entrée de données complexes de reparamétrisation en une seule action, au lieu de devoir ajuster séparément plusieurs points de contrôle. Le modèle d'interaction est profondément lié à la nature des informations traitées, puisque c'est en grande partie les techniques d'interaction utilisées qui sont à l'origine des structures de données choisies.

Nous retiendrons plus particulièrement trois particularités de la conception du modèle d'interaction :

* L'idée de base du modèle s'inspire de techniques éprouvées de dessin, et non du modèle de données utilisé. En fait, nous avons été amenés à redéfinir le modèle de données pour fournir une implantation efficace. Notre modèle de données est constitué de suites de segments contigus, et non des "formes" quelconques. Il est probable que si nous supposions un modèle différent, par exemple une grammaire de formes de bases (lignes, arcs de cercles, quadrilatères...), comme le font Saund et Moran [Saund et Moran 1994], notre technique d'interaction serait profondément modifiée.

* La plus grande difficulté de réalisation consiste à définir une fonction de distance entre segments de courbes qui confère une certaine prédictibilité à l'interaction. Il est difficile d'argumenter sur le choix que nous avons retenu. En tout état de cause, le choix d'une "bonne" distance est plus important que celui d'une bonne fonction de reparamétrisation, les modifications apportées à la courbe étant toujours relativement prédictibles.

* Dans une large mesure, Ligne Claire peut constituer une technique propre autour de laquelle il est possible de concevoir un outil complet de dessin, ayant son propre "toucher", son usage préférentiel et ses défauts (difficulté pour contrôler des propriétés géométriques telles que la continuité au-delà de C¹). Cette particularité rend l'évaluation et la comparaison quantitative avec d'autres techniques difficiles et hasardeuses. La meilleure évaluation qui puisse être portée sur Ligne Claire est son utilisation effective : est-ce-que des graphistes y trouveront un outil riche, leur offrant un potentiel d'expression important qu'ils sauront mettre en oeuvre ?

Ce dilemme de l'évaluation se pose très souvent, à des degrés plus importants encore, lorsque des logiciels radicalement nouveaux sont proposés. Ainsi, les tableurs ont révolutionné le domaine de la gestion. Le concept de tableur tient-il dans l'application, la structure de données et des fonctionnalités particulières offertes, ou dans l'interface proposée pour manipuler cette structure, la manipulation directe de colonnes et de rangées de chiffres ? Selon nous, les techniques de présentation et d'interaction ont certainement plus contribuées au succès des tableurs, qui sont, du point de vue de la structures de données, beaucoup plus pauvres que les bases de données relationnelles.